모델의 훈련 방식

훈련 데이터(Training Dataset)를 전부 사용해서 (1회) 학습시키는 방식을 Batch 훈련 방식이라고 한다.

In batch gradient descent, we use all our training data in a single iteration of the algorithm.

여기서 iteration의 의미는 학습 매개변수가 학습되는 일련의 과정을 의미한다. 즉, 10 times iterations은 학습 매개변수들이 10회 학습과정을 거쳤다는 의미다.

이와 대조적으로, 훈련 데이터셋 전체를 일정 갯수만큼(batch-size) 묶어서 소그룹(Mini-batch groups)별로 학습시키는 방식을 Mini Batch 훈련 방식 이라고 한다. 즉, 학습 파라미터들은 mini-batch group마다 1회 학습한다.

In Mini-batch gradient descent, we use a group of samples called mini-batch in a single iteration of the training algorithm.

Batch & Stochastic & Mini-batch Gradient Descent

경사 하강법 (Gradient Descent)으로 모델을 최적화한다고 생각해보자. 이 경우 앞서 언급한 Batch/Mini-Batch 방식을 포함해 일반적으로 크게 3가지 훈련 방식이 존재하게 된다.

Batch Gradient Descent, Stochastic Gradient Descent, Mini-batch Gradient Descent

Batch Gradient Descent(BGD): 모든 훈련 데이터 샘플들을 한번에 사용해서 그들의 평균 오차 기울기를 모든 학습 파라미터에 반영시키는 것.
Stochastic Gradient Descent(SGD): 훈련 데이터 샘플 각각에 대해서 오차 기울기를 각각 계산해서 학습시키는 것. 즉 100개 훈련 샘플이 있다면, 100번의 파라미터 학습이 이뤄진다.
Mini-batch Gradient Descent(MBGD): 훈련 데이터 샘플을 batch-size 크기(갯수)만큼 묶어서 batch group을 구성하고, batch group 마다 평균 오차 기울기를 계산해 학습시키는 것.

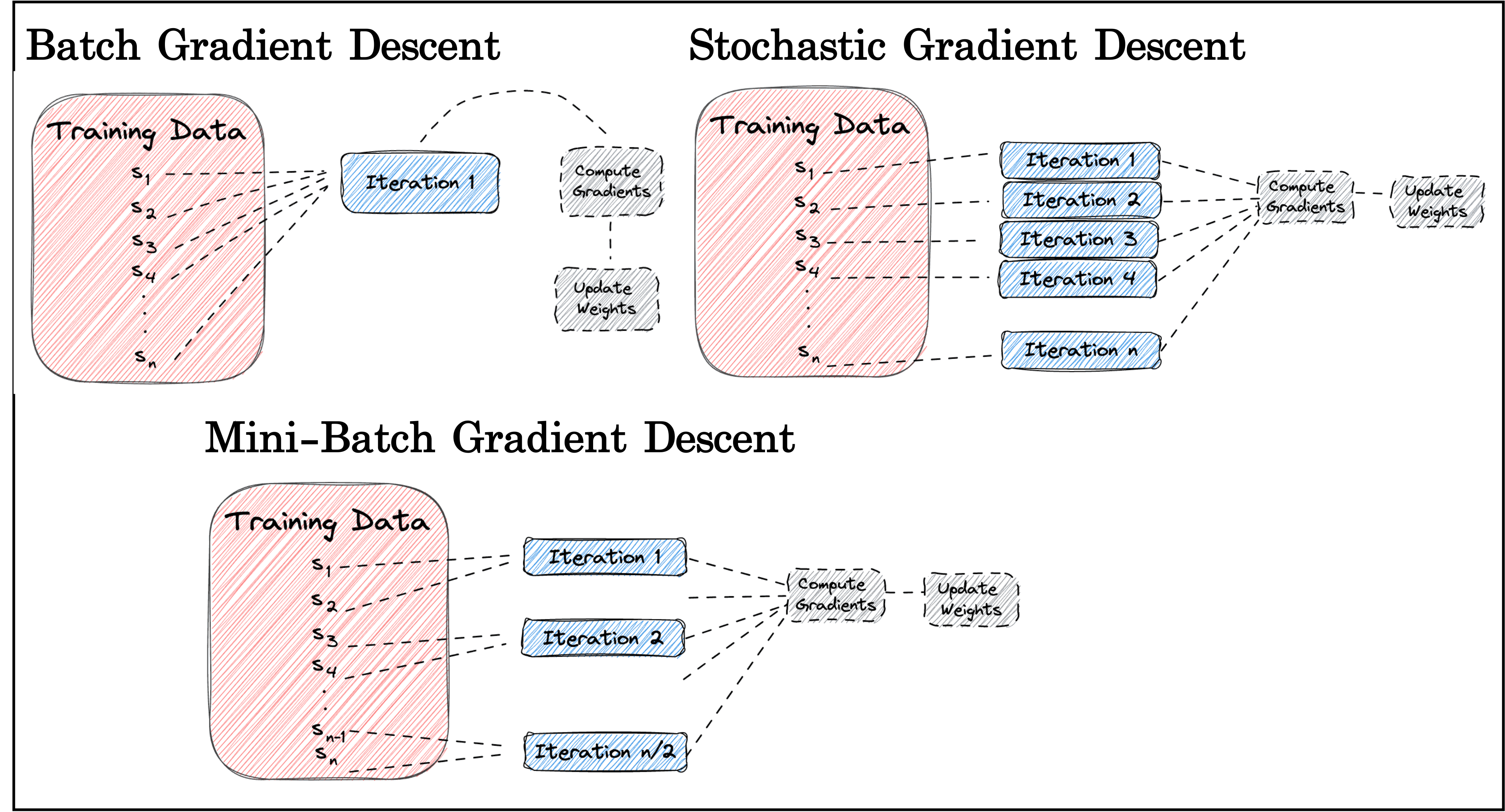“Differences Between Epoch, Batch, and Mini-batch”, Source: https://www.baeldung.com/cs/epoch-vs-batch-vs-mini-batch

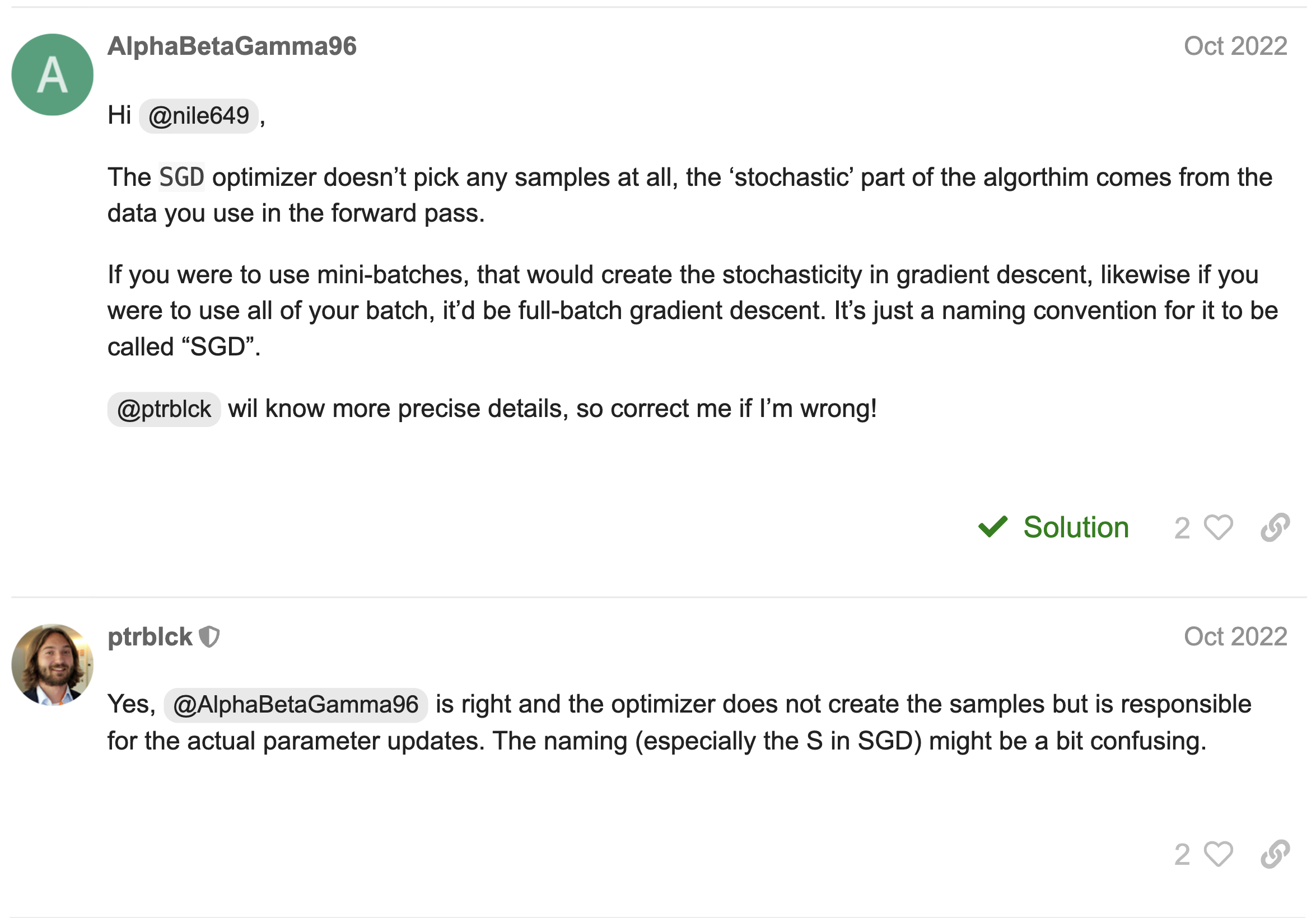
그럼에도 불구하고, 우리는 BGD든 SGD든 MBGD든 딥러닝 프레임워크에서 optimizer를 선택할 때 torch.optim.SGD()을 사용한다.

개념적으로 이렇게 완전히 다른 점과 모든 훈련에서 SGD optim을 사용한다는 점이 혼란스러워 커뮤니티 글을 찾아보니,,,, 일반적으로 Keras든 PyTorch든 Gradient Descent 최적화 알고리즘을 지칭할 때엔 ‘SGD’라는 용어로 통칭해 사용하는 것이 그냥 Convention, 관습이라고 한다.

즉, 모두 SGD optim을 쓰더라도, 전처리 과정에서 훈련 데이터를 batch-size만큼 묶어서 훈련시키면 그게 Mini-batch Gradient Descent방식이 되는거고, 반대로 모든 훈련 데이터를 입출력으로 한번에 사용(Full-batch)하면 그게 일반적인 Batch Gradient Descent가 되는거고, 마지막으로 훈련데이터 샘플을 한 개씩 모델에 순전파/역전파 시켜서 학습시키면 그게 Stochastic Gradient Descent 방식이란 소리다.

앞서 설명한 BGD/SGD/MBGD 개념대로 학습을 진행한다면, 대략 아래처럼 구현할 수 있다.

  
import torch
import torch.optim as optim
import torch.nn as nn
import torch.nn.functional as F

  
x_train = torch.randn(100, 1)
y_train = 3 * x_train + 2 + 0.5 * torch.randn(100, 1)

class LinearModel(nn.Module):
  def __init__(self):
    super().__init__()
    self.linear = nn.Linear(1, 1) # y = wx + b 선형 모델

  def forward(self, x):
    return self.linear(x)

  
model_bgd = LinearModel() # Full-batch size Gradient Descent를 수행할 모델
model_sgd = LinearModel() # Stoachastic Gradient Descent (훈련 샘플 한개씩) 수행할 모델
model_mbgd = LinearModel() # Mini-batch Gradient Descent를 수행할 모델

  
num_epochs = 200

# BGD
print("Batch Gradient Descent")
my_optim = optim.SGD(model_bgd.parameters(), lr=0.01)
for epoch in range(num_epochs+1):
  if epoch == 0:
    continue

  y_pred = model_bgd(x_train)
  cost = F.mse_loss(y_pred, y_train)

  my_optim.zero_grad()
  cost.backward()
  my_optim.step()
  if epoch % 20 == 0:
    print(f"Epoch: {epoch}/{num_epochs}, Cost: {cost:.4f}")
print()

# SGD
print("Stochastic Gradient Descent")
my_optim = optim.SGD(model_sgd.parameters(), lr=0.01)
for epoch in range(num_epochs+1):
  if epoch == 0:
    continue
  for i in range(len(x_train)):
    y_pred = model_sgd(x_train[i])
    cost = F.mse_loss(y_pred, y_train[i])

    my_optim.zero_grad()
    cost.backward()
    my_optim.step()

  if epoch % 20 == 0:
    print(f"Epoch: {epoch}/{num_epochs}, Cost: {cost:.4f}")
print()

# MBGD
print("Mini-batch Gradient Descent")
my_optim = optim.SGD(model_mbgd.parameters(), lr=0.01)
batch_size = 10
for epoch in range(num_epochs+1):
  if epoch == 0:
    continue
  for i in range(0, len(x_train), batch_size):
    y_pred = model_mbgd(x_train[i:i+batch_size])
    cost = F.mse_loss(y_pred, y_train[i:i+batch_size])

    my_optim.zero_grad()
    cost.backward()
    my_optim.step()

  if epoch % 20 == 0:
    print(f"Epoch: {epoch}/{num_epochs}, Cost: {cost:.4f}")

Batch Gradient Descent
Epoch: 20/200, Cost: 0.2246
Epoch: 40/200, Cost: 0.2246
Epoch: 60/200, Cost: 0.2246
Epoch: 80/200, Cost: 0.2246
Epoch: 100/200, Cost: 0.2246
Epoch: 120/200, Cost: 0.2246
Epoch: 140/200, Cost: 0.2246
Epoch: 160/200, Cost: 0.2246
Epoch: 180/200, Cost: 0.2246
Epoch: 200/200, Cost: 0.2246

Stochastic Gradient Descent
Epoch: 20/200, Cost: 0.0081
Epoch: 40/200, Cost: 0.0081
Epoch: 60/200, Cost: 0.0081
Epoch: 80/200, Cost: 0.0081
Epoch: 100/200, Cost: 0.0081
Epoch: 120/200, Cost: 0.0081
Epoch: 140/200, Cost: 0.0081
Epoch: 160/200, Cost: 0.0081
Epoch: 180/200, Cost: 0.0081
Epoch: 200/200, Cost: 0.0081

Mini-batch Gradient Descent
Epoch: 20/200, Cost: 0.2747
Epoch: 40/200, Cost: 0.2747
Epoch: 60/200, Cost: 0.2747
Epoch: 80/200, Cost: 0.2747
Epoch: 100/200, Cost: 0.2747
Epoch: 120/200, Cost: 0.2747
Epoch: 140/200, Cost: 0.2747
Epoch: 160/200, Cost: 0.2747
Epoch: 180/200, Cost: 0.2747
Epoch: 200/200, Cost: 0.2747

위 결과에선 문제 자체가 단순해서 인지하기 쉽지 않지만, 각각의 훈련 방식에는 장단점이 존재한다.

BGD: 한번에 모든 훈련 데이터에 대한 평균 오차 기울기를 반영하기에, iteration(학습)마다 Cost(Loss/Error)가 smooth하게 감소한다. 또한, 파라미터 학습에 모든 훈련 데이터 정보를 반영하기에, 적어도 train session 중엔, Global 또는 Local minimum으로의 수렴이 무조건 보장되어 있다. 단점으로는, 데이터 갯수가 많아지면 행렬곱 계산을 할 행렬 크기가 그만큼 커지는 셈으로 computational cost가 많아진다 (메모리 리소스 문제도 있고, 계산 속도도 느려지고 그러겠지).
SGD: 각 훈련 샘플마다 오차 기울기 계산 및 학습이 이뤄지고, 즉 개별 데이터 정보들이 모두가 오롯이 모델 학습에 반영된다. 이 말은, 모델이 더욱 자세하게(그렇다고 정밀하거나 정교하다는 의미는 아님) 미니멈 포인트를 탐색하며 학습할 수 있다는 의미고, 결과적으로 Generalization Error(= Out-of-sample Error)를 줄여준다. 다시 말해, 새로운 데이터에 대한 예측이 ‘비교적’ 정확해진다는 의미. 하지만 개별 데이터마다 Cost 역전파시키며 학습시키기에 결코 cost minimum 포인트에 도달할 수 없다. 그저 그 주위를 빙빙 맴돌며 학습이 이뤄진다. 게다가, 처리속도 측면에서도 개별 데이터 샘플마다 이뤄지는 계산 자체는 빠를지라도, 절대적으로 반복문(for-loop)을 통해 모든 데이터 샘플들을 순회해야 하므로 처리속도가 느려지게 된다. 이를 흔히 vectorization 이점을 취할 수 없다고 표현한다.
MBGD: 결국 BGD, SGD의 가장 큰 단점은 느리다는 것이다. 이 둘의 약점을 적절히 보완하면서, minimum 포인트로 유도하는 합리적인 방법이 바로 Mini Batch(Gradient Descent) 방식인 것이다. 훈련 데이터 전체를 적당한 갯수(batch-size)로 묶어서 학습을 진행하기에, 처리속도를 타협할 수 있다. 일반적으로, batch-size를 조절하며 시행착오들을 거쳐 적절한 batch size를 선정하게 된다. Batch size는 2,4,8,… $2^n$개로 고르는게 좋다고 한다. CPU/GPU의 메모리가 2의 배수라 배치크기를 $2^n$개로 해야 데이터 송수신의 효율을 높일 수 있다고 한다.

PyTorch: Mini-Batch 구현 방식

크게 torch.utils.data.TensorDataset와 torch.utils.data.DataLoader를 사용할 것이다.

TensorDataset은 Training & Test에 활용할 데이터셋을 PyTorch 프레임워크 안에서 유연하게 다룰 수 있도록 Wrapping 해주는 역할이라고 그냥 보면 된다.

TensorDataset으로 묶는 데이터셋은 torch.Tensor 타입 이어야 한다. 만약 Tensor 타입이 아니라 다른 유형의 데이터를 사용하려면, torch.utils.data.Dataset를 상속하는 커스텀 데이터 클래스를 만들어 사용하는 것이 일반적인 듯 하다.

DataLoader는 원하는 batch_size, shuffle (비)활성화 등에 맞게 데이터셋을 처리해주고, iterable 형태로 준비시켜주는 유용한 클래스이다.

shuffle 이라는 옵션은 epoch마다 데이터를 셔플시킬건지 설정하는 옵션이다. 매 epoch마다 동일한 순서로, 동일한 배치로 학습을 시키면 모델이 ‘문제와 답’ 사이의 관계보단 답의 ‘순서’에 익숙해질 수도 있다고 한다. »> default: False

  
x_train = torch.FloatTensor([[73,  80,  75],
                               [93,  88,  93],
                               [89,  91,  90],
                               [96,  98,  100],
                               [73,  66,  70]])
y_train = torch.FloatTensor([[152],  [185],  [180],  [196],  [142]])

  
dataset = TensorDataset(x_train, y_train)
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)

  
class LinearModel(nn.Module):
  def __init__(self):
    super().__init__()
    self.model = nn.Linear(3, 1)

  def forward(self, x):
    return self.model(x)

  
model = LinearModel()
my_optim = optim.SGD(model.parameters(), lr=1e-5)

  
num_epochs = 100
num_batches = len(dataloader) # 배치 그룹 갯수! batch_size가 아님.
for epoch in range(num_epochs):
  for batch_idx, samples in enumerate(dataloader):
    batch_x, batch_y = samples

    y_pred = model(batch_x)
    cost = F.mse_loss(y_pred, batch_y)

    my_optim.zero_grad()
    cost.backward()
    my_optim.step()

    if epoch % 10 == 0:
      print(f"Epoch: {epoch}/{num_epochs}, Batch: {batch_idx+1}/{num_batches}, Cost: {cost.item():.4f}")
  if epoch % 10 == 0:
    print()

Epoch: 0/100, Batch: 1/3, Cost: 13392.6035
Epoch: 0/100, Batch: 2/3, Cost: 5122.9238
Epoch: 0/100, Batch: 3/3, Cost: 2085.1494

Epoch: 10/100, Batch: 1/3, Cost: 8.4610
Epoch: 10/100, Batch: 2/3, Cost: 6.9835
Epoch: 10/100, Batch: 3/3, Cost: 25.6315

Epoch: 20/100, Batch: 1/3, Cost: 2.6494
Epoch: 20/100, Batch: 2/3, Cost: 9.6361
Epoch: 20/100, Batch: 3/3, Cost: 25.4140

Epoch: 30/100, Batch: 1/3, Cost: 6.6567
Epoch: 30/100, Batch: 2/3, Cost: 3.7038
Epoch: 30/100, Batch: 3/3, Cost: 28.4934

Epoch: 40/100, Batch: 1/3, Cost: 13.8477
Epoch: 40/100, Batch: 2/3, Cost: 6.1071
Epoch: 40/100, Batch: 3/3, Cost: 14.5157

Epoch: 50/100, Batch: 1/3, Cost: 15.1782
Epoch: 50/100, Batch: 2/3, Cost: 2.8699
Epoch: 50/100, Batch: 3/3, Cost: 13.8627

Epoch: 60/100, Batch: 1/3, Cost: 1.3499
Epoch: 60/100, Batch: 2/3, Cost: 16.2354
Epoch: 60/100, Batch: 3/3, Cost: 10.0041

Epoch: 70/100, Batch: 1/3, Cost: 1.6380
Epoch: 70/100, Batch: 2/3, Cost: 22.5639
Epoch: 70/100, Batch: 3/3, Cost: 9.9288

Epoch: 80/100, Batch: 1/3, Cost: 1.5055
Epoch: 80/100, Batch: 2/3, Cost: 22.2620
Epoch: 80/100, Batch: 3/3, Cost: 8.7638

Epoch: 90/100, Batch: 1/3, Cost: 6.8974
Epoch: 90/100, Batch: 2/3, Cost: 12.9072
Epoch: 90/100, Batch: 3/3, Cost: 5.6616

[PyTorch] Batch, Stochastic, Mini-Batch Gradient Descent

Table of Contents

모델의 훈련 방식

Batch & Stochastic & Mini-batch Gradient Descent

PyTorch: Mini-Batch 구현 방식

[PyTorch] Batch, Stochastic, Mini-Batch Gradient Descent

Table of Contents

모델의 훈련 방식

Batch & Stochastic & Mini-batch Gradient Descent

PyTorch: Mini-Batch 구현 방식

Further Reading

[PyTorch] Multi-Layer Perceptron & DNN - MNIST

Softmax의 안정성, Log Softmax, LogSumExp Function

[PyTorch] Classifier: Logistic & Softmax Regression Model