Table of Contents
Intro.
본 공부 내용은 유원준 님, 안상준 님이 저술하신 PyTorch로 시작하는 딥 러닝 입문 위키독스 내용들을 배경으로 하고 있습니다.
이번 글에서는 본격적인 MLP 모델, 심층 신경망(DNN) 모델을 PyTorch로 구현해보고 MNIST 데이터셋을 학습시켜본 내용을 기록하겠다.
앞선 글에서 구현한 입력층과 출력층으로만 구성된 모델 구조는 Singlelayer Perceptron, 즉 단층 퍼셉트론 구조라고도 불리는데, 단층 퍼셉트론 모델은 XOR 문제를 풀지 못하는 한계가 존재한다. 쉽게 말하면, 비선형적 표현이 불가능하다고 말할 수도 있고, 그냥 (시스템 및 대상에 대한) 모델의 표현력이 낮다 고도 말할 수 있다.
XOR 는 두 개가 서로 다른 논리 결과를 보일 때 True를 반환하는 연산자다. 예컨대, [True, False], [False, True]일 때 True를 반환. 반면 [True, True], [False, False]는 False를 반환.
1
2
3
4
5
6
7
8
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision.transforms as transforms
from torchvision.datasets import MNIST
from torch.utils.data import TensorDataset, DataLoader
from sklearn.model_selection import train_test_split
MNIST Dataset Load
1
2
3
mnist_dataset = MNIST(root='MNIST_data/',
download=True,
transform=transforms.ToTensor())
1
2
3
4
# Data size
mnist_dataset.data.shape
> torch.Size([60000, 28, 28])
1
2
3
4
5
x_train, x_test, y_train, y_test = train_test_split(mnist_dataset.data, mnist_dataset.targets, test_size=0.2, random_state=0)
print(f"훈련 데이터 갯수: {len(x_train):,}\n테스트 데이터 갯수: {len(x_test):,}")
> 훈련 데이터 갯수: 48,000
> 테스트 데이터 갯수: 12,000
1
2
3
4
5
6
7
# 정수형 데이터타입 [0, 255]의 입력 데이터셋을 [0, 1]값으로 정규화(Float 형으로 변환)
# 정규화를 안할 시, RuntimeError: mat1 and mat2 must have the same dtype, but got Byte and Float 에러 발생.
train_xy = TensorDataset(x_train/255, y_train)
test_xy = TensorDataset(x_test/255, y_test)
train_loader = DataLoader(train_xy, batch_size=64, shuffle=True, drop_last=True)
test_loader = DataLoader(test_xy, batch_size=64, shuffle=False, drop_last=False)
엄밀히 말하자면, 모델 test 과정에서 batch_size를 사용할 필요는 없다. batch_size로 data chunk 그룹을 나누는 것은 batch_size 크기만큼의 평균 오차로 전체적인 학습 방향성을 결정하는 일종의 학습 trick이기 때문이다. test 단계에서 batch_size를 지정하는 이유는 단지 데이터 크기가 너무 커서 이를 메모리에 전부 올리기 버거울 때 사용하는 것이다. 예컨대 앞선 글에서 설계한 SLP(Single Layer Perceptron) 모델의 테스트 단계에선 10000개의 test 데이터셋을 전부 model.forward()해서 inference를 수행했고, 그에 대한 계산이 순식간에 이뤄졌다. 하지만, 모델의 복잡도가 높은 MLP(Multilayer Perceptron) 모델과 훨씬 더 큰 테스트 데이터를 다룬다면, 이렇게 test 데이터셋에도 batch_size 그룹 단위로 추론을 수행하는 것이 계산 속도 및 메모리 안정성 측면에서 더 유리하다.
Multilayer Perceptron (MLP) Model
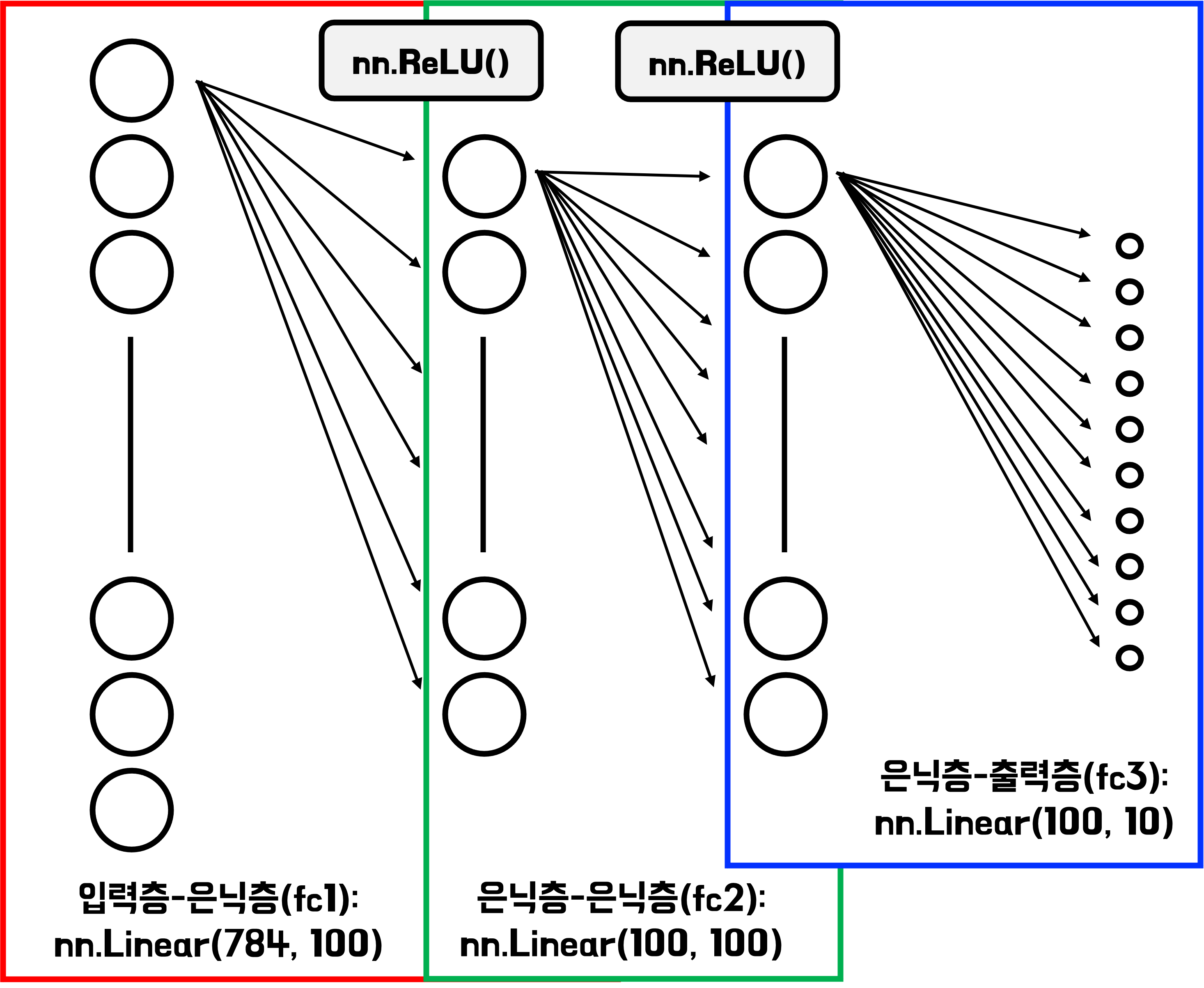
설계할 다층 퍼셉트론 모델(이른바 MLP 모델; Multilayer Perceptron)은 아래와 같은 구조다. 이전 글에서 MNIST 데이터 학습에 활용한 ‘입력 및 출력층으로만 구성된 단순 모델’(단층 퍼셉트론 모델; Singlelayer Perceptron 이라고도 함)과 달리 2개의 은닉층이 추가된 것을 볼 수 있다.
일반적으로 입력층과 출력층 사이에 은닉층이 1개 이상인 경우, 다층 퍼셉트론(MLP) 구조라고 부른다. 반면, 은닉층이 2개 이상인 모델의 경우, 그 구조를 심층 신경망(Deep Neural Network, DNN)이라고 부른다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 매뉴얼에서는 nn.Sequential().add_module()로 모델을 구현했는데,
# 이 글에서 나는 클래스로 표현하도록 하겠다.
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.fc1 = nn.Linear(28 * 28, 100)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(100, 100)
self.relu2 = nn.ReLU()
self.fc3 = nn.Linear(100, 10)
def forward(self, x):
x = self.relu1(self.fc1(x))
x = self.relu2(self.fc2(x))
x = self.fc3(x)
return x
1
model = MLP()
Optimizer and Loss Function
학습에 활용할 Optimizer와 Loss(or Cost) Function에 대한 인스턴스를 선언하고 이를 활용하자.
이번에 활용할 optimizer는 앞서 줄곧 실습에 활용하던 torch.optim.SGD()가 아니라, Adam optimizer를 사용할 것이다. Optimizer는 종류가 다양한데, 이들은 모두 loss minimum point를 어떤 전략(Optimizer)으로 찾아 나갈 것인지의 차이이다.
이들의 각기 다른 전략들, 즉 optimizer들은 학습 매개변수들을 어떻게 update시킬지의 차이이기도 하다. 기초적으로 다루는 Gradient Descent(경사하강법) 방식의 Optimizer인, torch.optim.SGD()는 학습시킬 매개변수 $\theta$ 를 아래와 같은 방식으로 update 시킨다.
\[\begin{equation} \theta_+ = \theta - \eta\nabla_{\theta}\mathcal{L\left(\theta\right)} \end{equation}\]loss function $\mathcal{L}$의 학습 매개변수($\theta$)에 대한 기울기를 학습률(learning rate) $\eta$와 곱해서 그 결과를 기존 $\theta$ 값에서 빼 $\theta_+$로 업데이트(학습)한다는 의미다.
반면, 그 외의 다른 optimizer들은 그들이 지닌 학습철학(?)에 따라 학습 매개변수를 업데이트하는 방식이 다르다. 아래 수식그림 참고.
Source: https://artemoppermann.com/optimization-in-deep-learning-adagrad-rmsprop-adam/
이 밖에도 종류가 다양하지만, 이 글에서는 Adam(Adaptive Moment Estimation)이라는 optimizer를 사용하고자 한다. Adam optimizer는 momentum과 RMSProp(Root Mean Square Propagation)의 전략을 결합한 학습방식인데, 거의 대부분의 딥러닝 문제들에 대해 효과적인 최적화 성능을 보이기에 2014년 발표 이후 지금까지도 대중적으로 사용하는 optimizer 중 하나이다.
인용수가 장난아니다…
1
2
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
Training
훈련하는 과정을 함수로서 define하고, 이 함수를 호출할 때마다 모델이 학습하도록 하자.
1
2
3
4
5
6
7
8
9
10
11
12
def train(current_epoch, total_epoch):
model.train(mode=True) # 아래에 설명
for x_data, y_data in train_loader:
x_data = x_data.reshape(-1, 28*28)
outputs = model(x_data)
optimizer.zero_grad()
loss = loss_fn(outputs, y_data)
loss.backward()
optimizer.step()
print(f"Epoch: {current_epoch+1}/{total_epoch}, Loss: {loss:.3f}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
num_epochs = 10
for epoch in range(num_epochs):
train(epoch, num_epochs)
>
Epoch: 1/10, Loss: 0.112
Epoch: 2/10, Loss: 0.165
Epoch: 3/10, Loss: 0.058
Epoch: 4/10, Loss: 0.048
Epoch: 5/10, Loss: 0.119
Epoch: 6/10, Loss: 0.025
Epoch: 7/10, Loss: 0.095
Epoch: 8/10, Loss: 0.076
Epoch: 9/10, Loss: 0.018
Epoch: 10/10, Loss: 0.013
이전 글에서 단층 퍼셉트론 모델(Singlelayer Perceptron; 입력층-출력층으로만 구성)로 MNIST 데이터를 학습했을 때보다 loss의 크기 수준이 시작부터 다르다.
단층 퍼셉트론 모델로 MNIST 를 학습했을 땐, 10회 epoch 만큼 학습시, 최저 loss가 0.27이었다. (물론 때에 따라 다르다)
학습모드와 평가모드
앞서 학습 함수를 정의할 때, 내부적으로 model.train(mode=True)을 먼저 선언했었다. 이것은 말그대로 학습 모드를 선언하는 것과 같다. 지금 이 모델에선 포함되지 않았지만, 실전 문제에선 대부분 모델의 Overfitting, Gradient Vanishing/Exploding 등의 문제들을 완화하기 위해 Batch Normalization, Drop-out 등의 Regularization 기법들을 사용한다.
Regularization은 모델의 복잡도를 줄이고 일반화 성능을 향상시키기 위해 추가적인 제약 조건을 모델에 부여하는 일련의 과정 및 행위들을 포괄하여 의미한다.
학습 과정에서 Batch Norm., Drop-out은 각각 각층의 입력 분포를 규격화(Normalization)시키기 위해 Batch statistics를 계산하고, 모델 구조의 일부가 일시적으로 없다 치고 학습을 진행하는 방식으로 동작한다.
이러한 동작들은 학습 모드일 때만 필요한 것이고, 학습 이후 평가 및 추론(Test) 단계에서는 비활성화되어야 하기 때문에, 이러한 모드 구분이 존재하는 것이다.
1
model.train(mode=True) # 학습 모드: default True임.
이렇게 선언하면, 이 정보들이 model 객체 내부에 있는 각 모듈들(layers, regularizer, etc.)을 학습 모드로 전환하는 것이다. PyTorch 문서 내 train 메서드 소스코드를 보면, 바로 이해가 갈 것이다. for문을 통해 model 내부 module들을 하나씩 모두 꺼내 학습모드로 설정하는 것을 볼 수 있다.
Source: https://pytorch.org/docs/stable/_modules/torch/nn/modules/module.html#Module.train
그럼, 평가 및 추론 단계에서 이들을 비활성화시키려면 어떻게 할까? 간단하다. model.eval()을 선언해주면 된다. model.eval()은 model.train(mode=False)와 완전히 equivalent하며, model 내부의 모든 module들의 학습모드를 비활성화시킨다.
Test
테스트 과정 역시 함수로 define하고, 이 함수를 호출할 때마다 현재 model 상태에서 test_loader에 담긴 테스트 데이터셋을 추론하고 정확도를 산출하도록 한다.
with torch.no_grad
평가 및 추론 단계에서는 model의 학습모드를 비활성화시키는 것 외에 사용하는 구문이 한 가지 더 있는데, 바로 torch.no_grad 구문이다.
이는 PyTorch의 Autograd engine을 비활성화시키는 역할을 수행한다. 파이토치의 Autograd engine은 모델의 forward 및 backward 모든 과정에서 텐서의 연산 흐름을 추적하고 Gradient 계산에 필요한 계산 그래프를 따로 구축한다. 궁극적으로 이러한 일은 평가 단계에서 필요하지 않기에, torch.no_grad()를 통해 비활성화시켜 메모리를 절약하고 계산 속도를 높이는 이점을 얻을 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def test():
model.eval() # model.train(mode=False)와 동일
correct = 0
test_size = len(test_loader.dataset)
with torch.no_grad(): # Autograd engine off
for x_data, y_data in test_loader:
x_data = x_data.reshape(-1, 28*28)
outputs = model(x_data)
batch_correct = sum(torch.argmax(outputs, dim=1) == y_data)
correct += batch_correct
print(f"테스트 데이터셋에서 예측 정확도: {correct:,}/{test_size:,} ({correct/test_size * 100:.2f} %)")
1
2
3
test()
> 테스트 데이터셋에서 예측 정확도: 11,693/12,000 (97.44 %)
Visualization
그림을 안그리고 마무리하면 아쉬우니, 테스트 데이터셋에서 샘플 몇개를 뽑아 시각화 결과와 함께 보자.
1
2
3
import matplotlib.pyplot as plt
temp_test_loader = DataLoader(test_xy, batch_size=10, shuffle=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
model.eval()
with torch.no_grad():
for x_data, y_data in temp_test_loader:
x_flatten = x_data.reshape(-1, 28*28)
outputs = model(x_flatten)
predicted_labels = torch.argmax(outputs, dim=1)
break
fig, axs = plt.subplots(nrows=2, ncols=5, facecolor='w', figsize=(15, 6))
for i, ax in enumerate(axs.flatten()):
test_img = x_data[i].reshape(28, 28)
ax.imshow(test_img, cmap='gray')
ax.set_title(f"Label: {y_data[i]}, Predict: {predicted_labels[i].item()}", fontsize=12)
ax.axis('off')
plt.suptitle("MLP INFERENCE RESULTS", fontsize=25)
plt.subplots_adjust(wspace=0.2, hspace=0.2)
plt.show()
